精品亚洲a∨无码专区毛片-精品亚洲aⅴ无码午夜在线-精品亚洲aⅴ无码午夜在线观看-精品亚洲aⅴ无码一区二区三区-精品亚洲aⅴ无码专区毛片-精品亚洲aⅴ在线

1.引言

       在研究晶體振蕩器和原子鐘的穩(wěn)定性時，人們發(fā)現(xiàn)這些系統(tǒng)的相位噪聲中不僅有白噪聲，而且有閃爍噪聲。使用傳統(tǒng)的統(tǒng)計工具（例如標準差）分析這類噪聲時統(tǒng)計結果是無法收斂的。為了解決這個問題，David Allan于1966年提出了Allan方差分析，該方法不僅可以準確識別噪聲類型，還能準確確定噪聲的特性參數(shù)，其優(yōu)點在于對各類噪聲的冪律譜項都是收斂的。該方法初被用于分析晶振或原子鐘的相位和頻率不穩(wěn)定性，比如，晶振的中心頻率均采用Allan方差來表征時域內(nèi)的穩(wěn)定度。由于gao端陀螺，氣體傳感等各類物理量測儀器本身也具有晶振的特征，因此該方法隨后被廣泛應用于各種物理傳感器的隨機誤差辨識中。

這些是本文即將涵蓋的主題。

       下文中，我們首先將從整體上介紹傳感器噪聲的基礎知識。有了噪聲知識，我們將討論Allan方差圖的含義，幫助你在購買產(chǎn)品中使用這些數(shù)據(jù)進行決策以及在使用產(chǎn)品時校正傳感器的噪聲。

2.信號，噪聲和數(shù)據(jù)

2.1.噪聲

       這只是一個純粹的定義，但將對我們的分析很有幫助。如果這個定義不正確，則信號中不趨近于零的部分就不是“噪聲”，而是其他的東西。可能是某種干擾，可能是傳感器的偏移量，甚至，可能就是你要測量的數(shù)據(jù)！信號中不是噪聲又不是實際數(shù)據(jù)的部分通常稱為“錯誤”。在現(xiàn)實世界中的數(shù)據(jù)流（即信號）中，所有這些因素和其他因素共同構成了傳感器輸出的值。以加速度計為示例：

       即使這樣，我們也無法使用單個數(shù)據(jù)點來很好地校正噪聲。首先，噪聲水平通常是“大”噪聲。這意味著噪聲將偏離實際數(shù)據(jù)值約0.01g，但其幅度也可能更小。即使我們假設噪聲始終為0.01g，該特定數(shù)據(jù)點上的噪聲是疊加還是降低？換句話說，我們的測量值實際上是1.062還是1.042？沒有辦法知道。

測量噪聲

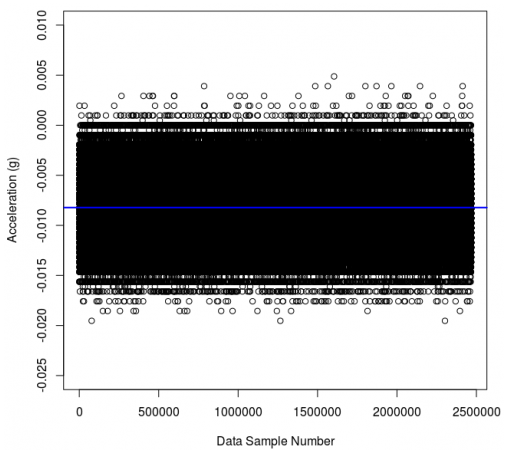
       如果將所有這些值取平均值，我們將得到沿藍線的值。它非常接近零，為-0.008。這里可能涉及到準確性的問題（我們將在今后的文章中介紹有關準確性Accuracy和分辨率Resolution的定義和應用）。但是由于該傳感器已經(jīng)過校準，因此上述偏差的原因更可能是由于加速度計相對于地球重力矢量略有傾斜引起的，這會導致加速度在X或Y方向上存在一定的分量。

       但是，你可能會想：這種分析僅在我們不想測量任何變化的數(shù)據(jù)時才會有效。因為你買加速度計可不只是為了測重力，你實際上希望它能夠移動——在真實應用環(huán)境中測量加速度隨時間的變化。為此，我們需要表征噪聲隨時間變化的情況，因此需要找出能夠校正噪聲之前，要采集數(shù)據(jù)的時間長度。

3.Allan方差

       對于許多傳感器而言，存在一段理想的時間長度，在該時間長度上取平均值（或其他統(tǒng)計參數(shù)）可以獲得噪聲的小值（至少對于某些類型的噪聲）。以上面的250萬個點為例，我們可以問一個問題：要以較高的信噪比達到-0.008的期望值，我們需要至少平均多少個點？這是一個很好的問題，但不幸的是，對于所獲取的數(shù)據(jù)集，直到獲得很多數(shù)據(jù)點之后，我們才知道-0.008這個“答案”。

       現(xiàn)在，我們將每個單獨的數(shù)據(jù)點視為一個“組”，而不是由125萬個點組成的兩組。也就是說，我們現(xiàn)在有250萬個“組”。在這種情況下，我們做同樣的事情——“平均”每個組（在這種情況下，每“組”只有一個數(shù)據(jù)），然后檢查所有組平均值之間的方差。當將每個單獨的點視為一個“組”時，組平均值的方差就等于傳感器在以每個點的平均時間為間隔時的噪聲。以上述傳感器為例，兩側的平均值大約為0.01g（總計0.02g）。

       為此，我們不僅要有一個或125萬個小組，而且要嘗試所有組的規(guī)模。因此，我們可以遍歷整個數(shù)據(jù)集，并將其分成由2個數(shù)據(jù)點構成的組，然后分別平均。然后以3，4，5 .... 10 .... 100 .... 1000等個數(shù)據(jù)點為組，分別進行平均。后我們找到所有大小相等的數(shù)據(jù)組之間的方差。隨著數(shù)據(jù)組變得越來越長，不同數(shù)據(jù)組之間的平均值會越來越接近，因為每個數(shù)據(jù)組的平均值會越來越接近“真實”的平均值。

       幸運的是，網(wǎng)上已經(jīng)有很多程序可以讓我們做Allan方差計算。其文檔和資源可在線獲得。我們利用這些程序可得到如下圖：

       該圖顯示了我們期望的結果（即，確實存在一個非常明顯的點，對足夠大的一組數(shù)據(jù)求平均會使噪聲水平比數(shù)據(jù)數(shù)量較少的組小）。但是，這個圖并不是非常有用，有兩個原因：

• 這種變化過于劇烈，以至于很難說出理想的組數(shù)是多少 

• 方差的單位是傳感器值的平方，而“加速度平方”不是一個很直觀的單位 

還有一個奇怪的事實是，方差在下降之后會再次上升，我們稍后再來討論這點。

       不過，我們可以通過將數(shù)據(jù)放在對數(shù)——對數(shù)圖上來解決di一個問題。下降之所以如此急劇，是因為方差在較短的橫軸區(qū)間內(nèi)下降了幾個數(shù)量級。因此，對數(shù)——對數(shù)圖將給較小的數(shù)字更大的權重，并加重變化。我們可以使用Origin或者Matlab將上述數(shù)據(jù)重新作圖，將橫軸和縱軸都更改成對數(shù)坐標，從而得到如下圖：

       在di一個線性圖中方差的平方增加對應對數(shù)——對數(shù)圖中的顯著轉折。即使在線性圖上，也可以清楚看到與初始的噪聲降低相比，噪聲也只是略有上升的趨勢。