Allan方差是什么?(下)
4.Allan偏差
對數——對數圖的使用僅僅解決了“計算”部分中描述的一個問題。另一個問題——方差的單位為“平方”,這使我們無法解釋對數——對數圖曲線上對應的Y值的概念。
為了解決這個問題,我們可以使用Allan偏差(標準偏差或標準差)而不是Allan方差。偏差是方差的平方根,因此要從Allan方差中得出Allan偏差,只需取上面計算出的每個方差的平方根即可。這會將數據單位改回我們可以直觀理解的單位(即傳感器實際記錄的單位——加速度單位)。
但是,標準偏差的含義比方差要更難理解一點。方差是數據集合的整體分布統計,而標準差只是數據中與平均值接近的68%的數據的分布統計。比如,如果平均值是0,而標準偏差是正負5,則該數據集的大約32%大于5且小于-5。因此,方差告訴你highest和低范圍,標準差僅告訴你大部分數據位于何處。
也就是說,偏差圖更一目了然。
我們可以通過計算Allan方差的平方根,然后得到如下的Allan偏差圖:
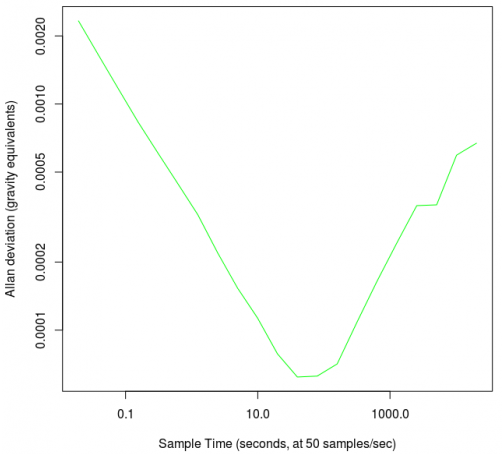
5.如何使用Allan偏差圖
使用Allan偏差圖比較產品或學習如何使用傳感器時,可以將圖中的曲線分為四個部分。當然網上還有其他有關如何解釋這些圖的教程。為了將不同類型噪聲的影響分開,其中一些教程將Allan偏差圖分成了更多部分。對于此處的實際討論,我們省去了有關不同類型噪聲的許多細節。常見的Allan偏差圖的四個部分如下:
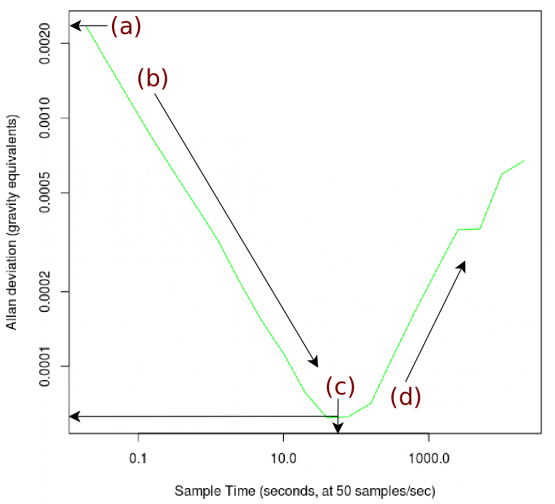
我們將在下面更深入地討論所有這四個部分:
A點——對應的Y值是任何一次測量的噪聲的標準偏差,或者以單個數據點間隔為平均時間的噪聲。
B段——表示隨著平均時間的增長,平均值標準偏差逐漸減小,可用于校正快速波動的噪聲。
C點——終,通過延長平均時間,噪聲可以達到一個小值。該小值具有用戶感興趣的optimal平均時間X和小系統噪聲(或信噪比為1時的靈敏度)Y值,C點也就是前文提到的“大信噪比”所需的平均時間。
D段——在較長時間范圍內的慢變噪聲或系統漂移占主導,開始影響較大組的平均數據。
5.1. A點——單點噪聲
Allan偏差圖的起點是單個點的噪聲標準偏差。因為在圖的開始處, “組”的大小為1。因此,組與組之間變化的標準偏差將等于各個點的標準偏差。因此,通過對比所計算數據集的起始Allan偏差和各個點的標準偏差,可以初步確認Allan偏差計算的準確性。
請注意,對于偏差(漂移)不大于白噪聲的情況,上述描述是正確的。如果偏差隨時間的漂移比短時間內白噪聲產生的漂移大,則數據集的標準偏差將是測量偏差,而不是白噪聲標準偏差。
用于選擇產品
在比較產品時,A點數值對需要盡可能少的平均數據的應用場景有很大價值。即,用戶需要盡可能多的使用每個數據點,或者需要盡可能多的保留數據中的高頻分量。對于大多數應用,如“噪聲”部分所述,至少進行一些平均是非常有用的。
實際應用
使用傳感器時,此值在嘗試評估單個測量點的噪聲時很有用。大約68%的測量結果將產生0.0025g的噪聲誤差,而32%的測量結果將具有更大的噪聲誤差。正如“噪聲”部分中所述,要確定單個測量數據點的噪聲是大是小,是正是負,實際上是不可能的。因此,將A點數值與你期望獲得的測量值幅度進行比較,以及噪聲誤差是否會成為測量數據的重要分量,會對實際應用非常有幫助。
5.2. B段——通過平均來改善精度
隨著你可以收集越來越多的數據,并將它們取平均,你可以對數據進行精度更高的提取。
用于選擇產品
要使用從A點的大值到C點的小值的B段區間,你需要考慮自己的應用場景。你可以合理采樣和平均的時長是多少?你是否想要每0.1秒獲取讀數或每1秒一次獲取讀數?如果你的應用試圖在Allan偏差圖中測量相對于噪聲非常小的信號,則需要在可平均的時間范圍內,比較不同產品的Allan偏差圖。
實際應用
在可允許的采樣運算時間內,通過調整平均時間的長度,抑制每單位時間的降噪量,優化系統的信噪比,同時保證系統足夠的響應速度,可以幫助你更準確的微調應用場景中的數據采樣和平均時間間隔。
例如,在很多四軸飛行器的應用中,通過適當平滑加速度計的輸出數據,以抑制其跳躍性的噪聲,可以幫助你更準確地估計GPS讀數之間的飛行器位置。對于加速度數值遠大于噪聲的情況而言,平均可以稍微平滑這些噪聲,但不會影響加速度計輸出結果的準確性。因此,只要你感興趣數據的價值足夠大,且平均時間足夠長而不會受到太大影響,則可以收集到更多的數據樣本來更有效地過濾噪聲。這種偏差建模——通過延長平均時間法——允許你沿著B段斜率向下移至一個系統可接受的響應平均時間的小值。
但是,對于測量比采樣頻率更快的振動信號,這種方法將不再起作用。
5.3. C點——小偏差(optimal靈敏度)
理論上,此小偏差是傳感器的optimum精度。實際應用中,即使要達到這一水平也可能是很困難的。為此,你必須以約等于小C點的平均時間處理數據。這需要非常特定的應用程序和采樣策略。
對于例子中的加速度傳感器,optimum靈敏度大約是每100秒平均一次,每秒50個采樣,也即采集5000個點平均一次獲得的。請記住,optimum靈敏度只是噪聲的標準偏差,因此,即使在C點的輸出,也將有大約三分之一的噪聲大于圖中顯示的小值。
用于選擇產品
Allan偏差圖上的optimal靈敏度值,是比較不同傳感器常用的特征點。該數據點的用途是向你顯示靈敏度optimum的情況。根據Allan偏差圖,你可以選擇采取不同的采樣時間,并且在所需的靈敏度上有多少回旋余地(平均會大大提升傳感器的靈敏度),但請記住,你的數據仍會在C點小值附近產生偏差。事實上,在選擇產品時,圖形上的所有點都具有價值的。
5.4. D段——低頻噪聲
當你在此低頻噪聲中僅取一小部分值(例如隨機噪聲)時,數值變化會非常小。在越來越大的數據組中,隨機噪聲可能會很大。該噪聲通常是多個因素的疊加,包括溫度的影響,振動和隨機游走等。
像其他噪聲一樣,真正隨機噪聲終將平均為零。但是,你將必須收集非常非常長時間的數據。足夠長的時間可以保證你的數據捕獲任何合理的重復頻率的隨機噪聲。但是,想象一下——假設你發現新的小噪聲點超過了數萬秒的平均時間——你是否真的想對所有這些數據進行平均以確定小偏差?這樣做,你會錯過所有來自傳感器的真實,快速的數據,因為你一直都在等待采集足夠的數據做長期平均值。
用于選擇產品
即使要在曲線的較早一點進行平均,該圖的這一部分仍然非常重要。這是由于這樣的事實,無論平均周期如何,你仍然會經歷隨機或溫度依賴形式的低頻噪聲。想象一下,一組1000個數據點的中值在整個過程中緩慢漂移。如果將每十個數據點平均一次,則可能會減輕大部分白噪聲,但數據仍將漂移至以前相同的量。
在Allan偏差上做一個與X軸平行的直線,該線與Allan偏差曲線交于e和f兩點,如下圖所示。e點和f點雖然平均時間不同,但是檢測精度其實是相同的。如果這個Allan偏差曲線右端對應的Y值高于左端first的Y值,說明到達此點時間后,系統已經漂移超過原始未平均的靈敏度。
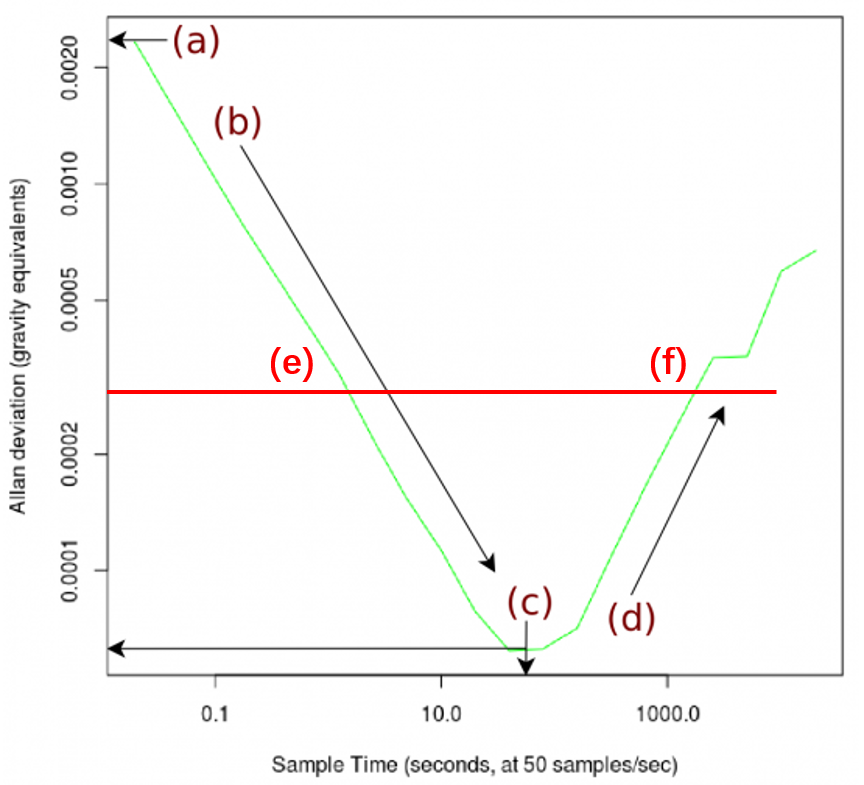
如果你對傳感器和所收集的數據有非常清楚的了解,則可以使用軟件算法校正和處理低頻噪聲,但這是很困難的,只能根據具體情況進行。如果這種操作在你的應用中不可行,則選擇低頻噪聲曲線較淺的傳感器將很有價值。當然,你會發現傳感器的低頻噪聲與傳感器的成本直接相關。
6.溫度的影響
當溫度變化時,電子系統會經歷一定程度的誤差變化(溫飄),終反映在噪聲特性中。當查看加速計數據隨時間變化時,這些溫度影響并不是立即顯而易見的,例如“測量噪聲”部分中的圖形。
但是溫漂效應和其他較小的難以控制的影響使慣性導航變得極為困難。如果在室溫下記錄加速度計的Allan偏差圖,則低頻噪聲特性(曲線上的D段)可能不會非常陡峭。但是,如果你使用相同的加速度計并將其置于動態溫度環境中,則會發現低頻噪聲曲線將變得更加陡峭或難以預測。通過比較這兩個Allan偏差圖,并使所有其他變量保持恒定,你可以大致確定溫度變化對設備的影響有多大。
 您好, 歡迎來到化工儀器網
您好, 歡迎來到化工儀器網

 5
5